The emergence of temporal earthquake clusters in a 1D rate and state friction model with a sinusoidal driving velocity. The orange line is the harmonically varying driving velocity and the blue line shows the cumulative fault displacement accrued through multiple earthquake cycles.

One of the reasons that earthquake prediction is hard is that the occurrence of large earthquakes is rarely periodic (Berryman et al., 2012). Paleoseismic records of earthquake activity have been interpreted as consistent with the temporal clustering of large earthquakes in relative compressed time intervals within longer intervals that are sometimes called “supercycles” (Sieh et al., 2008) and two-dimensional numerical models have been developed to explain these observations (e.g., Barbot, 2020).

A second, and seemingly independent observation, is the recent interpretations of geodetic data as containing low magnitude monthly- (Bedford et al., 2020) to centennial-scale (Meneses-Gutierrez et al., 2022) deviations from steady plate motion rates. These works have analyzed contemporary and historical data and revealed small magnitude (~5-10%) variations surface motions over large (>100 km) length scales.

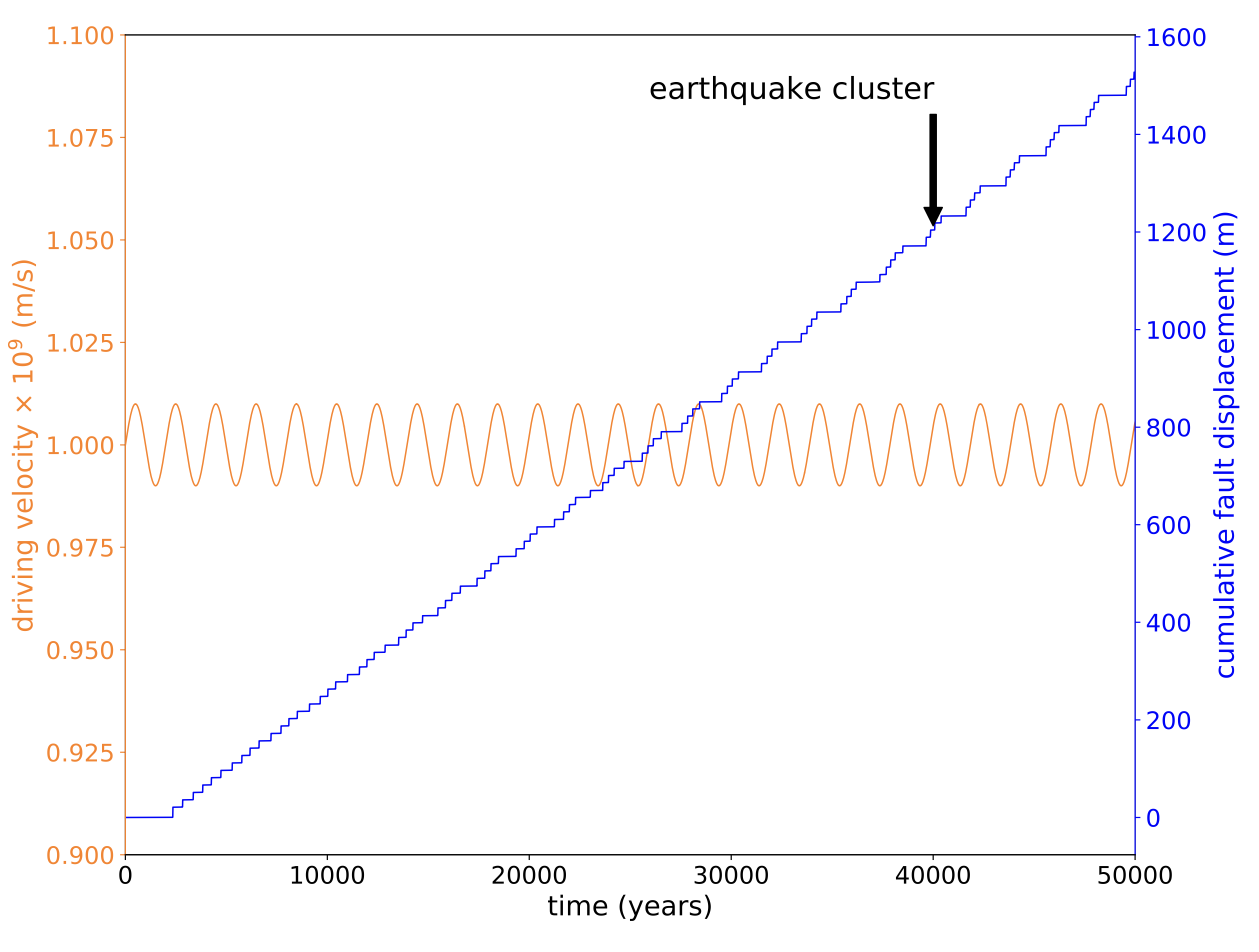
Here we describe a simple low-dimensional explanation for the emergence of temporally clustered earthquakes (supercycles) as a result of rate and state friction with harmonic time variable loading (inspired by the geodetic observations described above). The model (link to colab) is the classical one-dimensional spring slider rate and state friction model with the aging law (e.g., Ruina, 1983) which produces a series of earthquakes that occur periodically. We modify this on one small way: Introducing a sinusoidally varying driving velocity, \(V_p = \sin(t/ T)\) where \(T\) is the period of oscillation (orange line in the figure above). Here the period of oscillation is approximately 300 years and the amplitude of the perturbation is 1%. In this case earthquakes initially to occur periodically as they do in the steady forcing case. However, after a period of time (approximation 30,000 years in this example) a new pattern emerges characterized by a sequence of 4 earthquakes occurring in relatively rapid succession (blue line in the figure above) followed by a period of prolonged quiescence (~1000 years). This is analogous to the temporal pattern of large seismic events associated with supercycles.

There is nothing exotic here and nothing not previously known from prior numerical experiments. Rather this is a highly idealized model simple numerical model that potentially offers a simple quantitative link between recent paleoseismic and geodetic observations.